| Type |
BA, SA |
| Supervisor |
Prof. Dr.-Ing. Alois Knoll |
| Advisor |
Markus Weißmann, M.Sc. |
| Research Area |
Boolean Algebra, Optimization |
| Programming Language |
OCaml |
| Required Skills |
OCaml API design |
| Required Knowledge |
Boolean Algebra |
| Language |
English or German |
Description
Boolean algebra expressions are used in a phletora of fields. Often it is desired that these expressions take a minimal form, e.g. in
- design of circuit diagramms.
- optimization of algorithms
- reduction of problems in verification
For example the expression
A and (B or A) is equivalent to just
A, the expression
A and (not A) is equivalent to
false, etc.
As the problem itself is NP-complete, there are no efficient algorithms for it. There exist different algorithms to find an optimal solution (e.g. Karnaugh-Veitch-diagramms, Quine McCluskey) as well as heuristic based ones (e.g. Espresso).
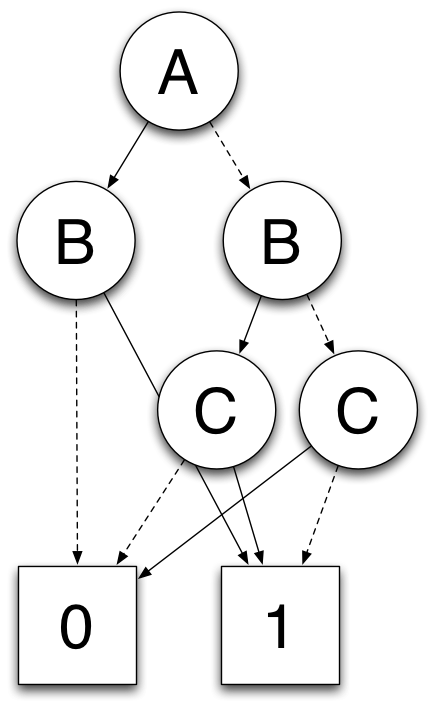
The goal of this project is to create a library that provides multiple algorithms to reduce boolean algebra expressions.
The library should have a common interface for all implemented algorithms so that the concrete algorithm can be changed very easily.
This will make it easy to chose an appropriate algorithm for the concrete problem.
For more information, contact
Markus Weißmann.
Literature
- Donald E. Knuth: The Art of Computer Programming, Volume 4, Fascicle 1: Bitwise Tricks and Techniques; Binary Decision Diagrams, Addison-Wesley Longman, 2009
- McGeer, P.; Sanghavi, J.; Brayton, R.; Vincentelli, A.S (1993).: ESPRESSO-SIGNATURE: A New Exact Minimizer for Logic Functions, 30th Conference on Design Automation, 618-624
- Espresso PLA Solver C-Sources
- McCluskey (1956): Minimization of Boolean Functions. Bell System Technical Journal, 35, 14171444.
- Giovanni DeMicheli: Synthesis and Optimization of Digital Circuits, Mcgraw-Hill, 1994
